The basic idea behind FlashAttention

Note: The majority of this article is derived from these course notes by Zihao Ye.

In a Transformer’s attention layer, computing the entire attention matrix for an input with a long sequence length can result in a lot of memory usage. Recall that the basic operations in a single head of attention look something like this. (In PyTorch, with regularization techniques like dropout omitted for brevity)

B, T, C = x.shape
# Linear/projection layers that go from d_model to d_head
q = self.query(x)
k = self.key(x)
v = self.value(x)

# att is of shape (T, T)
att = q @ k.transpose(-2, -1) * k.shape[-1]**-0.5 # Pre-softmax logits
att = att.masked_fill(self.tril[:T, :T] == 0, float('-inf')) # Self-attention mask
att = F.softmax(att, dim=-1)

out = att @ v

The attention matrix is of shape (T, T), which for long sequence length can be very large. This generally would not fit into on-chip memory, necessitating storage in global memory, which is much slower. Even worse, a naive safe softmax implementation would have to read from the attention matrix (pre-softmax logits) three times in order to compute the output probabilities. This exacerbates the problem.

FlashAttention is an algorithm that allows us to compute the output out from q, k, v without having to materialize the entire attention matrix att at any one point. How does it work?

Online Softmax

FlashAttention is based on the Online Softmax algorithm from this paper where it is listed as Algorithm 3. The naive “safe” or numerically stable softmax implementation requires 3 passes over the input vector, which has length $N$:

1. First pass: Obtain the max $m$ across all elements $x_i$. This is needed to “debias” all terms by the maximum value of $x_i$ to avoid overflow when the exponential function is applied.
2. Second pass: Compute the denominator $d$ by summing the terms $e^{x_i -m}$
3. Third pass: Compute the probability for each element by calculating $e^{x_i-m}\over{d}$

Online Softmax reduces this to two passes by merging the first and second passes into one, so that in a single pass we compute both the max $m$ and the denominator $d$. (The third pass is unchanged)

This is done by keeping track of the current max $m_i$ on each iteration and also a running total representing the “partial” denominator, $d_i$.

Then using techniques from discrete math, a recurrence relation is found between $d_{i-1}$ and $d_i$, so that the partial denominator is “updated” based on the new current max $m_i$. (These course notes go through the exact derivation)¹

The merged first and second passes end up looking like this: For each iteration $i$: $$ m_i = \text{max}(m_{i-1}, x_i) $$ $$ d_i = d_{i-1}e^{m_{i-1} - m_i} + e^{x_i - m_i} $$ In the calculation of the partial denominator of $d_i$, the factor $e^{m_{i-1} - m_i}$ that is used to multiply $d_{i-1}$ represents a “correction” to update the debiasing of all previous terms in the partial denominator. The terms had previously been $e^{x_i- m_{i-1}}$, so multiplying them by this factor transforms them to be $e^{x_i - m_i}$, which is now properly debiased by the current maximum.

Then, the terminal values $m_N$ and $d_N$ represent the maximum of $x_i$ and the denominator, respectively.

In Python the code would look something like this:

import math
def online_softmax(x):
  # Initial values
  m = float('-inf')
  d = 0
  for x_i in x:
    m_next = max(m, x_i)
    d = d * math.exp(m - m_next) + math.exp(x_i - m_next)
    m = m_next
  o = []
  for x_i in x:
    o.append(math.exp(x_i - m) / d)
  return o

Reducing the number of passes over the input is important, because this can translate into fewer memory accesses.

FlashAttention

To understand how the concepts from the Online Softmax algorithm can help with the attention mechanism, let’s first review how it works.

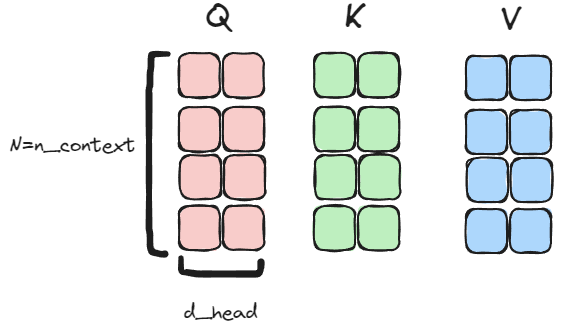
First, we start off with the Query (Q), Key (K) and Value (V) matrices. The shapes are all (N=n_context, d_head), which in this example is (4, 2):

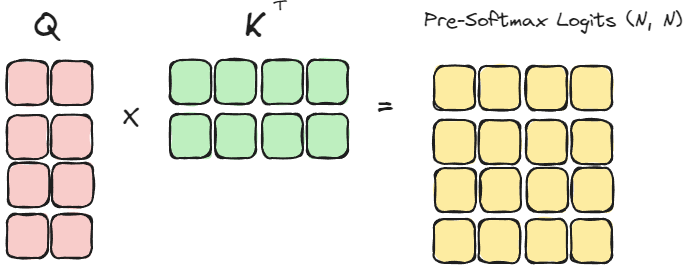
We then perform Q @ K.transpose() to compute the attention pre-softmax logits, which is a matrix of size (N, N)

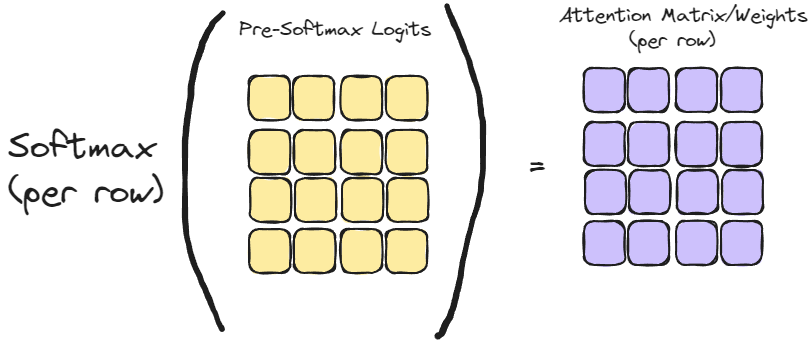
Then the Softmax (row-wise) function is applied to compute the attention matrix:

Finally, the attention weights are applied to the value matrix to obtain the output.

Each row of the attention matrix corresponds to the weights applied to each row in the value matrix, so that each row in the output matrix is a weighted sum of the rows in the value matrix. This is more evident, if we just consider a single row in the attention matrix:

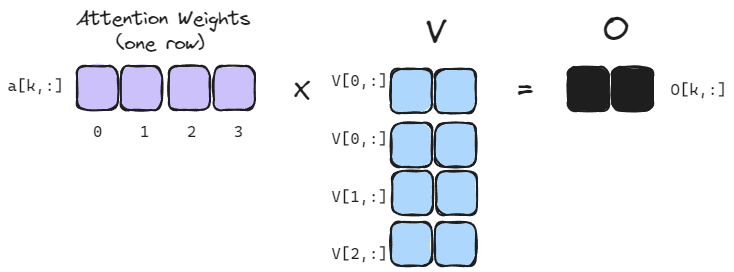
For the attention mechanism, we actually don’t care about computing of the attention weights (each row in the attention matrix) all at once. We are only concerned with computing the final matrix (O) of output vectors. That is, if we label a single attention row as $a[k,:]$ and the $N$ rows of $V$ as $V[i, :]$, then we only care about the accumulated sum:

$$ O[k, :] = \sum_i^N{a[k,i]V[i,:]} $$ We don’t care about producing the entire attention row $a[k,:]$ at once. Because of this, the FlashAttention is able to collapse the the process into a single pass per output row, vs. the two passes required of online softmax.

This is done by iterating $i$ over $N$ (length of context) and doing the following: ²

1. Compute $x_i$ as $Q[k,:]K^T[:,i]$: This is the $i$-th element in the $k$-th row of the pre-softmax attention matrix
2. Compute the “running max” $m_i$ as $\text{max}(m_{i-1}, x_i)$ (As done in online softmax)
3. Compute the partial/running denominator as $d_i = d_{i-1}e^{m_{i-1} - m_i} + e^{x_i - m_i}$. (As done in online softmax)
4. Update and accumulate the result into in the output $o$: $$ \begin{equation} \begin{split} o_i= o_{i-1} ({d_{i-1}\over{d_i}} e^{m_{i-1} - m_i}) + {e^{x_i-m_i}\over{d_i}}V[i,:] \end{split} \end{equation} $$
5. At the end of the loop, the final value $o_N$ is equal to the output row $O[k,:]$

In the equation in point (4):

1. The factor $({d_{i-1}\over{d_i}} e^{m_{i-1} - m_i})$ is the amount we “adjust” the previously-accumulated values in $o$ by. Essentially, we factor out the previous partial denominator $d_{i-1}$ and then divide by the current denominator $d_i$. Then, we also apply the correction $e^{m_{i-1} - m_i}$ to update the max value used to debias $x_i$, as was done in online softmax
2. The second term ${e^{x_i-m_i}\over{d_i}}V[i,:]$ represents the weighted value of the row $V[i,;]$ based on the current maximum $m_i$ and current partial denominator $d_i$.

This loop computes the output of one row $O[k,:]$ but it can be easily parallelized across different values of $k$.

The code for this basic FlashAttention algorithm looks something like this:

# For processing ONE query row against `n_ctx` k, v rows.
# Naive iterative solution for ease of understanding.
# For brevity, masking and scaling have been left out.
import torch
torch.manual_seed(1337)
d_head = 10
n_ctx = 5

q = torch.randn((d_head,))
k = torch.randn((n_ctx, d_head))
v = torch.randn((n_ctx, d_head))
# output should be same size as q
o = torch.zeros_like(q)

m = torch.tensor(float('-inf'))
d = torch.tensor(0)

for i in range(n_ctx):
  x_i = q @ k[i:i+1, :].transpose(-2, -1)
  m_next = torch.maximum(m, x_i)
  d_next = d * torch.exp(m - m_next) + torch.exp(x_i - m_next)

  # Update the output:
  # 1. o_adjust is the factor which we adjust existing output by based on previous/current values of m, d
  # 2. o_add is the weighted value of i'th row of v to add in based on current values of m, d
  o_adjust = d * torch.exp(m - m_next) / d_next
  o_add = torch.exp(x_i - m_next) * v[i:i+1, :] / d_next
  o = o * o_adjust + o_add
  m = m_next
  d = d_next

# At the end of the loop:
# 1. m will have the max across x_i (but not need)
# 2. d has the denominator (but not need)
# 3. o will have the result of aggregating across the rows of v using attention scores

c = F.softmax(q @ k.transpose(-2, -1), dim=-1) @ v
print(f'Result:\n{o=}')
print(f'Correct should be:\n{c=}')
print(f'Result is correct? {torch.allclose(o, c)}')

This code could be translated into a single GPU kernel (aka “kernel fusion”) rather than calling separate kernels for each step of attention, and incurring the cost of writing to/reading from global memory in between each step.

With this approach, we never actually materialize the entire attention matrix, nor even a single full row of it at once. In fact, in the attention mechanism, the attention matrix is an intermediate value that we don’t actually care about - we only care about the actual output matrix $O$. By avoiding materializing the entire attention matrix, this improves memory efficiency by avoiding having to write and then subsequently read a large matrix to/from global memory.